Question

What are Gamma function and power function models?

Answer 1

Gamma Function (Γ Function)

Definition and Properties

The gamma function is an extension of the factorial function over real and complex numbers, denoted by Γ(x). Its core definition is given by the integral form:

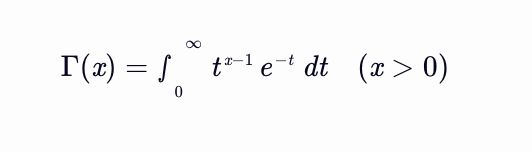
This function is widely used in analysis, probability theory, partial differential equations, and combinatorics. For example, it is used to normalize probability density functions (such as the gamma distribution) and to compute generalized values of factorials (Γ(n) = (n-1)!, where n is a positive integer).

Key Features

Recurrence relation: Γ(x+1) = xΓ(x), which allows for fast computation of non-integer factorials.

Covariate formula: Γ(x)Γ(1-x) = \frac{\pi}{\sin(\pi x)}, which simplifies complex integrals.

Special value: Γ(1/2) = \sqrt{\pi} (Wallis formula).

Smoothness: Γ(x) is infinitely differentiable, and its derivatives can be expressed using higher-order derivative formulas. Application Scenarios

Probability Theory: Normalizing constants for Beta and Gamma distributions.

Physics: Computing wave function integrals in quantum mechanics.

Engineering: Fourier transform coefficients in signal processing.

Power Function Model

Definition and Form

A power function is a function of the form

y=x^a

,where α is a real constant. Its domain and image shape vary significantly with the exponent α:

When α > 0:

The image passes through the origin (0, 0) and (1, 1).

It increases monotonically on the value [0, +∞), and its derivative increases (concave) when α > 1 and decreases (convex) when 0 < α < 1.

When α < 0:

The image passes through (1, 1) and decreases monotonically on (0, +∞).

It has two asymptotes (coordinate axes): the function value approaches +∞ as the independent variable approaches 0, and approaches 0 as it approaches +∞.

When α = 0:

Degenerates to the constant function y = 1 (x ≠ 0).

Parameter Influence Mechanism

Domain: Determined by the value of α. For example:

When α is a natural number, the domain is ℝ;

When α is a negative integer, the domain excludes the origin;

When α is a fraction, the domain is [0, +∞) when the denominator is even, and ℝ when the denominator is odd.

Parity: Determined by the parity of α. For example:

When α = 3, it is an odd function, and its graph is symmetric about the origin;

When α = 4, it is an even function, and its graph is symmetric about the y-axis.

Application Areas

Physics: Inverse square law (e.g., the law of universal gravitation).

Economics: Analysis of scale effects (e.g., the production function).

Y=AX^a

Biology: Allometric growth equations (e.g., the relationship between animal metabolic rate and body weight to the power of 3/4).

Engineering: Material strength calculations (e.g., the power law model of the stress-strain curve). The gamma function is a special function that extends the concept of factorials and is suitable for complex calculations in continuous domains. The power function model, using the exponent α to characterize nonlinear relationships between variables, is widely used in analyzing power law phenomena in both natural and social sciences.

Both complement each other in terms of mathematical tools and application scenarios, and together constitute important components of function theory.

Answer 2

The power function model is a mathematical model that describes the power relationship between two variables. Its general form is y=ax², where y and x are variables, a is the coefficient with a=0, and n is a real number. By adjusting the coefficient a and the exponent n, the model can flexibly fit different types of data trends, such as linear growth (n=1), quadratic growth (n=2), cubic growth (n=3), or more complex nonlinear relationships. Even when n is a negative number, the model can describe situations where y gradually decreases as x increases, such as an inverse proportional relationship (n=−1). In various fields such as natural sciences, social sciences, and economics, the power function model is widely used to describe physical phenomena, population growth, and economies of scale.

Its advantages lie in its simplicity and universality, and it can capture the essential relationships between variables with a relatively small number of parameters. However, its use requires attention to its assumptions, such as the need to verify the power relationship between variables based on actual data.

Answer 3

The gamma function is an extension of the factorial function to real and complex numbers, defined as Γ(x) = ∫[0, +∞] t^(x-1) e^(-t) dt (x>0). It has the recursive property Γ(x+1) = x * Γ(x), and when x is a positive integer, Γ(x) = (x-1)!. In probability theory and statistics, it is used to normalize probability density functions, such as the gamma distribution. The power function model is of the form y=x^a (α is a constant), and its properties are closely related to the value of α. When α>0, the power function is monotonically increasing on (0,+∞), and its graph passes through the points (1,1) and (0,0). When α<0, the power function is monotonically decreasing on (0,+∞), and its graph passes through the point (1,1). In the first quadrant, as x increases, the function value approaches 0. In physics, the power function is used to describe ideal models such as the relationship between the distance and time of a falling object.

Answer 4

The gamma function model is a mathematical tool that describes the properties of the gamma function. As an extension of the factorial to the real domain, the gamma function is defined as Γ(z) = ∫[0, +∞] t^(z-1) e^(-t) dt (for z>0). Its core properties include the recurrence relation Γ(z+1)=zΓ(z) (similar to the factorial with n!=n×(n−1)!), its connection to the factorial with Γ(n)=(n−1)! (when n is a positive integer), and its analytical extension to the complex domain. This model is widely used in probability theory (e.g., describing inter-event times with the gamma distribution), statistics (conjugate priors in Bayesian analysis), physics (wave function normalization in quantum mechanics), and engineering (filter design in signal processing). Its advantage lies in its ability to handle non-integer parameters continuously, overcoming the discrete nature of the factorial, while maintaining mathematical analyticity and computational feasibility through its integral form. It serves as an important bridge between discrete mathematics and continuous analysis.